Vogel’s Approximation Method (VAM) | Method to Solve Transportation Problem | Transportation Model
Watch videoVogel's Approximation Method (VAM) is one of the method to obtain feasible solution of Transportation Problem. We already know the Least Cost Method and the North West Corner Method | Method to Solve Transportation Problem | Transportation Model for transportation problem to obtain feasible solution.
Vogel's Approximation Method (VAM) method works on the concept of Opportunity or Penalty cost.
Opportunity cost is the penalty occurring for not selecting the right cell for the allocation.
We will learn how to find Opportunity cost later in this note only, while going through different steps of the numerical presented here.
To understand Vogel's Approximation Method we will go through the numerical provided as follows (the same numerical we used in North West Corner Method | Method to Solve Transportation Problem | Transportation Model and Least Cost Method:
Numerical
A mobile phone manufacturing company has three branches located in three different regions, say Jaipur, Udaipur and Mumbai. The company has to transport mobile phones to three destinations, say Kanpur, Pune and Delhi. The availability from Jaipur, Udaipur and Mumbai is 40, 60 and 70 units respectively. The demand at Kanpur, Pune and Delhi are 70, 40 and 60 respectively. The transportation cost is shown in the matrix below (in Rs). Use the Vogel’s Approximation Method to find a basic feasible solution (BFS).
Note that all the explanation is provided in “CYAN” colour. You have to write in examination the only thing which are given in this regular colour under each steps(if any), else you can directly solve matrix of the problem as explained here.

Solution:
Step 1: Balance the problem
Balance the problem meaning we need to check that if;
If this holds true, then we will consider the given problem as a balanced problem.
Now, what if it’s not balanced?
If such a condition occurs, then we have to add a dummy source or market; whichever makes the problem balanced.
You can watch this video on Unbalanced Transportation Problems for these kinds of numericals.
The given transportation problem is balanced.

Step 2: Find out the Row difference and the Column difference
Now, we will find out the row and the columnn difference of the provided matrix.
Note: Row/Column difference is known as Opportunity or penalty cost. Thus, by finding out the difference in each row and column, we are finding Opportunity cost here.
As the value of difference is larger, higher will be the penalty for allocating in second smallest cost cell instead of smallest cost cell of that particular row/column in the matrix.
So, this indicates penalty for wrong allocation.
For the same we will solve this as follows:
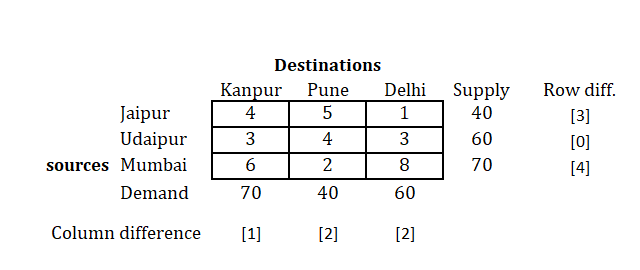
Here as you can see in the first row, we need to find out cell containing smallest value (least cost we can say), and then from the rest two values, find the smallest.
Hence, we find 1 and 4 as the smallest values in the first row.
Take the difference of this two numbers, i.e. .
Similarly, find out differences for all the rows as shown above.
Also, we will be doing the same procedure with columns.
So, for the first column, you will get, .
Find out difference for all columns in the same manner.
Step 3: Select the row/column with highest difference
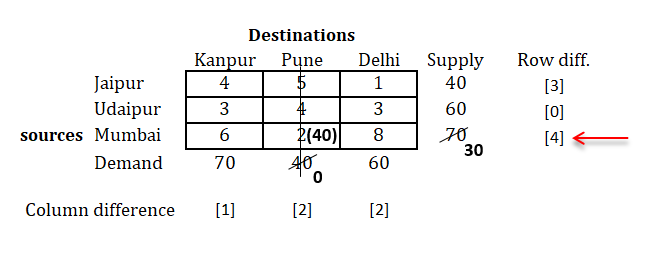
As we can see above the highest difference value is 4, for the last row.
So we will select that row, and find out the minimum cost in that row.
You will find that, minimum cost is 2.
Now, comparing supply and demand for this row and column respectively.
We find that, we have supply as 70 and demand as 40 for the selected cell.
Comparing both and selecting minimum of them for the allocation in the cell, as shown below.
Check out the column whose demand is fulfilled.
Step 4: Remove the row/column whose supply or demand is fulfilled and prepare new matrix and repeat the same procedure
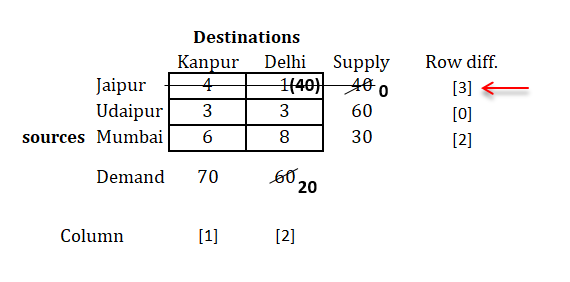
As you can see, we have now new matrix with second column removed (as its demand was 40 and it's fulfilled)
Now, we will repeat the same procedure untill we're done with all allocations.
i.e.,
- Find row and column difference.
- Select highest difference.
- Allocate cell with minimum cost, associated with selected highest row or column difference.
- Check out row/column, if demand or supply is fulfilled.
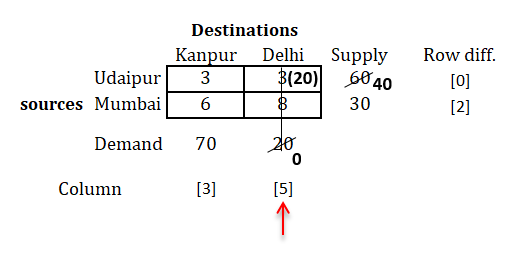

Tip:
→ As you can see in the above last step, there no row and column difference provided.
→ Its becuase we have only two cells left, and you can select any of this cell first, it doesn't matter.
→ Also, if you find difference and do the same procedure, it will lead you to the same answer.
This will help to save your time in eaxmination.
Step 5: After all the allocations are done, write all the allocations in the matrix and find Transportation cost
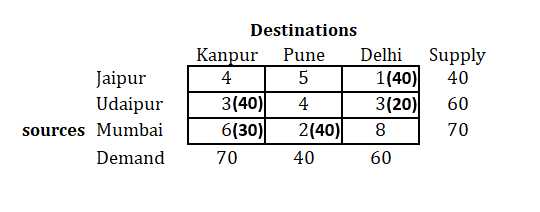
We have all allocations with their respective cell now.
Find transportation cost as follows:
You may find solution of this numerical by VAM and Least cost method as same , but that's not always possible.
Actually, VAM is more effective method than the other two (Least Cost Method & North West Corner Method | Method to Solve Transportation Problem | Transportation Model).
We recommend you to use Vogel's Approximation Method in examination, if there is no specific method mentioned in the question.
Wondering what if there's tie in selecting the difference or allocation cell ???
Check this video for the same - Tie in selecting Row and Column - Vogels approximation method (VAM), also notes for the same will be uploaded soon. Subscribe to notifications, to get notified with latest update on EL Website.
The notes for above mentioned video is now available - Tie in selecting row and column (Vogel's Approximation Method - VAM) | Numerical | Solving Transportation Problem | Transportation Model
Find solution of same numerical by:
Suggested Notes:
Modified Distribution Method (MODI) | Transportation Problem | Transportation Model
Stepping Stone | Transportation Problem | Transportation Model

Transportation Model - Introduction
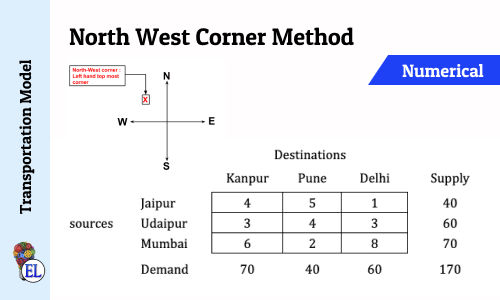
North West Corner Method | Method to Solve Transportation Problem | Transportation Model
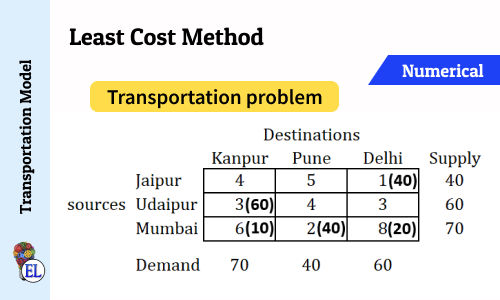
Least Cost Method | Method to Solve Transportation Problem | Transportation Model
Tie in selecting row and column (Vogel's Approximation Method - VAM) | Numerical | Solving Transportation Problem | Transportation Model

Assignment Model | Linear Programming Problem (LPP) | Introduction

Crashing Special Case - Multiple (Parallel) Critical Paths

Crashing Special Case - Indirect cost less than Crash Cost

Basics of Program Evaluation and Review Technique (PERT)

Numerical on PERT (Program Evaluation and Review Technique)

Network Analysis - Dealing with Network Construction Basics

Construct a project network with predecessor relationship | Operation Research | Numerical
Graphical Method | Methods to solve LPP | Linear Programming
Basics of Linear Programming

Linear Programming Problem (LPP) Formulation with Numericals

Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment