PQ = 12cm and PR = 13cm | Find tan P - cot R | Trigonometry Numerical
Watch videoQuestion: Given a right triangle PQR, where m∠Q = 90°, PQ = 12 cm and PR = 13 cm, find the value of tan P - cot R.
 fig. 1
fig. 1
Explanation
To find the value of , we need to calculate the values of tan P and cot R using .
From the formulas that we learnt in the notes of basics of trigonometry, we get
Similarly, doing the same for cot R, we get
From equation (1) and equation (2), we will require the values of side QR and side PQ. But as we do not have the value of QR, we'll first apply Pythagoras Theorem on and find the value of QR.
Solution
We know that is a right angled triangle, hence applying Pythagoras Theorem we get
Putting the values of PQ and PR in the above equation to find the value of

Now that we have the value of QR, we can find the value of equation that is asked in the question
Bonus section
Quick tip #1 (to find the value of the problem)
Sometimes these kinds of questions can be asked for only 1 mark as MCQ, so it might not be required to show such a long calculation. So here's a short explanation on how to quickly solve such kinds of questions.
You can start from what is asked in the question, like so:
Let's assume the value of to be . Hence we get the equation as:
Quick tip #2 (to calculate the third side of a right angled triangle)
There is a term in Mathematics known as Pythagorean triples. A pythagorean triple is a set of three positive integers that can be written in the form of . Some of the well known Pythagorean triples are
- (3, 4, 5)
- (6, 8, 10)
- (5, 12, 13)
For any Pythagorean triple, the addition of squares of the two smallest values would be equal to the square of the largest value in that triple. And that is what the equation says.
Whenever you are dealing with a right angled triangle where two of its sides are known and are in a need to find the third side, try to solve it using Pythagorean triples.
In the question above, we have the largest side, hypotenuse, as PR (13 cm) and one other side PQ (12 cm). We can directly apply the Pythagorean triple (5, 12, 13) and know that the remaining side of the triangle i.e. QR will be 5 cm.
Note that, you can apply Pythagorean triple only when dealing with a right angled triangle.
Suggested Notes:

tan (A + B) = √3 and tan (A -B) = 1/√3 | Trigonometry Numerical
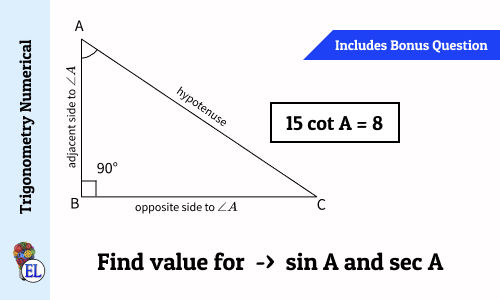
15 cot A = 8 | Find the value of sin A and sec A | Trigonometry Numerical

cot θ = 7/8 | Find all other trigonometric ratios | Trigonometry Numerical

Trigonometry Formulas | sin θ, cos θ, tan θ, cosec θ, sec θ, cot θ | Trigonometry Basics

Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment